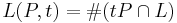Ehrhart polynomial

In mathematics, an integral polytope has an associated Ehrhart polynomial which encodes the relationship between the volume of a polytope and the number of integer points the polytope contains. The theory of Ehrhart polynomials can be seen as a higher-dimensional generalization of Pick's theorem in the Euclidean plane.

These polynomials are named after Eugène Ehrhart who studied them in 1960s.

Contents 1 Definition 2 Examples 3 Interpretation of coefficients 4 Related topics 5 See also 6 Notes 7 References

Definition

Informally, if P is any polyhedron or polytope, and tP is the polytope formed by expanding P by a factor of t in each dimension, then L(int P, t) is the number of integer lattice points in tP.

More formally, consider a lattice L in Euclidean space Rⁿ and a d-dimensional polytope P in Rⁿ, and assume that all the vertices of the polytope are points of the lattice. (A common example is L = Zⁿ and a polytope with all its vertex coordinates being integers.) For any positive integer t, let tP be the t-fold dilation of P (the polytope formed by multiplying each vertex coordinate, in a basis for the lattice, by a factor of t), and let

be the number of lattice points contained in tP. Ehrhart showed in 1962 that L is a rational polynomial of degree d in t, i.e. there exist rational numbers a₀,...,a_d such that:

L(P, t) = a_dt^d + a_d−1t^d−1 + … + a₀     for all positive integers t.

The Ehrhart polynomial of the interior of a closed convex polytope P can be computed as:

L(int P, t) = (−1)ⁿ L(P, −t).

Examples

If P is a d-dimensional unit hypercube whose vertices are the integer lattice points all of whose coordinates are 0 or 1, then the t-fold dilation of P is a cube with side length t, containing (t + 1)^d integer points. That is, the Ehrhart polynomial of the hypercube is L(P,t) = (t + 1)^d.^[1]

Many other figurate numbers can be expressed as Ehrhart polynomials. For instance, the square pyramidal numbers are given by the Ehrhart polynomials of a square pyramid with an integer unit square as its base and with height one; the Ehrhart polynomial in this case is (t + 1)(t + 2)(2t + 3)/6.^[2]

Interpretation of coefficients

If P is closed (i.e. the boundary faces belong to P), some of the coefficients of L(P, t) have an easy interpretation:

• the leading coefficient, a_d, is equal to the d-dimensional volume of P, divided by d(L) (see lattice for an explanation of the content or covolume d(L) of a lattice);
• the second coefficient, a_d−1, can be computed as follows: the lattice L induces a lattice L_F on any face F of P; take the (d−1)-dimensional volume of F, divide by 2d(L_F), and add those numbers for all faces of P;
• the constant coefficient a₀ is the Euler characteristic of P. When P is a closed convex polytope, a₀ = 1.

Related topics

The case n = d = 2 and t = 1 of these statements yields Pick's theorem. Formulas for the other coefficients are much harder to get; Todd classes of toric varieties, the Riemann–Roch theorem as well as Fourier analysis have been used for this purpose.

If X is the toric variety corresponding to the normal fan of P, then P defines an ample line bundle on X, and the Ehrhart polynomial of P coincides with the Hilbert polynomial of this line bundle.

See also

• Quasi-polynomial

Notes

References

• Beck, M.; De Loera, J. A.; Develin, M.; Pfeifle, J.; Stanley, R. P. (2005), "Coefficients and roots of Ehrhart polynomials", Integer points in polyhedra—geometry, number theory, algebra, optimization, Contemp. Math., 374, Providence, RI: Amer. Math. Soc., pp. 15–36, MR2134759 .
• Beck, Matthias; Robins, Sinai (2007), Computing the Continuous Discretely, Integer-point enumeration in polyhedra, Undergraduate Texts in Mathematics, New York: Springer-Verlag, ISBN 978-0-387-29139-0, MR2271992 .
• De Loera, Jesús A.; Rambau, Jörg; Santos, Francisco (2010), "9.3.3 Ehrhart polynomials and unimodular triangulations", Triangulations: Structures for Algorithms and Applications, Algorithms and Computation in Mathematics, 25, Springer, p. 475, ISBN 9783642129704, http://books.google.com/books?id=SxY1Xrr12DwC&pg=PA475&lpg=PA475 .
• Diaz, Ricardo; Robins, Sinai (1996), "The Ehrhart polynomial of a lattice n-simplex", Electronic Research Announcements of the American Mathematical Society 2: 1–6, doi:10.1090/S1079-6762-96-00001-7, http://www.ams.org/era/1996-02-01/S1079-6762-96-00001-7/home.html . Introduces the Fourier analysis approach and gives references to other related articles.
• Ehrhart, Eugène (1962), "Sur les polyèdres rationnels homothétiques à n dimensions", C. R. Acad. Sci. Paris 254: 616–618 . Definition and first properties.
• Mustaţă, Mircea (February 2005), "Chapter 13: Ehrhart polynomials", Lecture notes on toric varieties, http://www.math.lsa.umich.edu/~mmustata/toric_var.html .